WG2 - Nonlinear problems
Overview
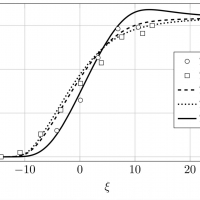
Often, linear models are first-order approximations in the descriptions of intricate phenomena. Their study is a mandatory first step whose results open the way to more accurate portraits of the problems being studied. On the other hand, general nonlinear equations typically generate a variety of behaviours that can hardly be described and classified along the lines of their linear counterparts. In this context, numerical integrations, or experiments, play a crucial role. They are often the only tool available to have a first insight into the qualitative behaviour of the solutions to the various nonlinear models.
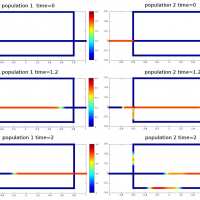
This project aims at a maximal exploitation of the known linear theories to obtain relevant information on specific nonlinear models. A prime example is offered by a class of predator-prey models that leads to mixed hyperbolic-parabolic systems consisting of equations that, when seen separated, are linear. In addition, various models based on differential equations will be considered. The physical settings will be diverse, comprising, for instance, biological or traffic models, as well as the more traditional fluid dynamics models, such as those based on Boltzmann equation.
Tasks
- Fully develop a semigroup approach for nonlinear DSNs in a general metric space setting (in collaboration with W1 And W4).
- Develop appropriate nonlinear perturbation results.
- Study stability questions for the nonlinear case.
- Nonlinear models of microscopic, macroscopic and kinetic nature.
- In collaboration with WG5 develop suitable numerical methods for applications.