C0 - semigroups and beyond
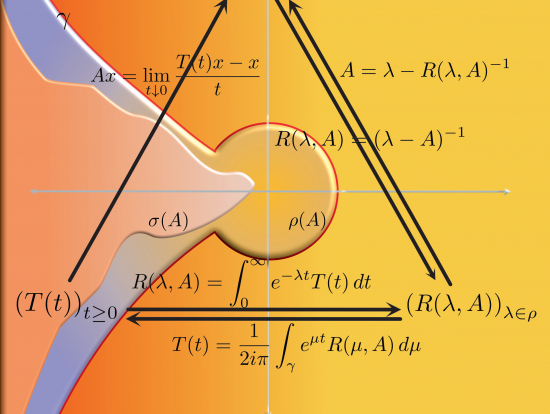
The theory of C0-semigroups, time-continuous linear dynamical systems, is a useful tool to study evolution equations. There is a one-to-one correspondence between these objects and well-posed abstract Cauchy problems on Banach spaces.
Nonlinear problems
Often, linear models are first-order approximations in the descriptions of intricate phenomena. Their study is a mandatory first step whose results open the way to more accurate portraits of the problems being studied.
Networks and similar structures
The cell cycle, as well as the exploitation of a biological resource or demographic models, lead to renewal equations (i.e., balance laws with possibly nonlocal boundary conditions) on graphs. Their analytic treatment has some features that resemble that of models for vehicular traffic on road networks.
Variational methods on graphs and networks
Proceeding from classical variational methods for the analysis of Laplace-type operators, the aim of this Working Group is twofold.
Numerical methods and applications
Since the differential equations which arise in applications like cell cycle, biological resource and demographic models, or vehicular traffic on road networks have a rather complicated structure, the analytical approach to the analysis of the dynamics of the corresponding system is not viable.
