CA18232 - Mathematical models for interacting dynamics on networks
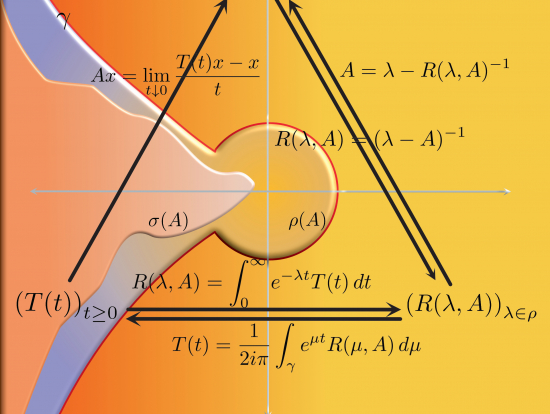
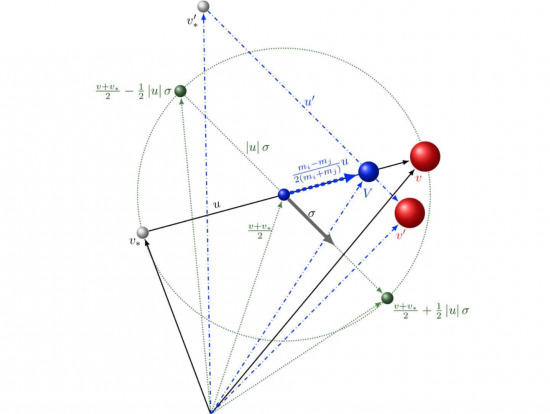
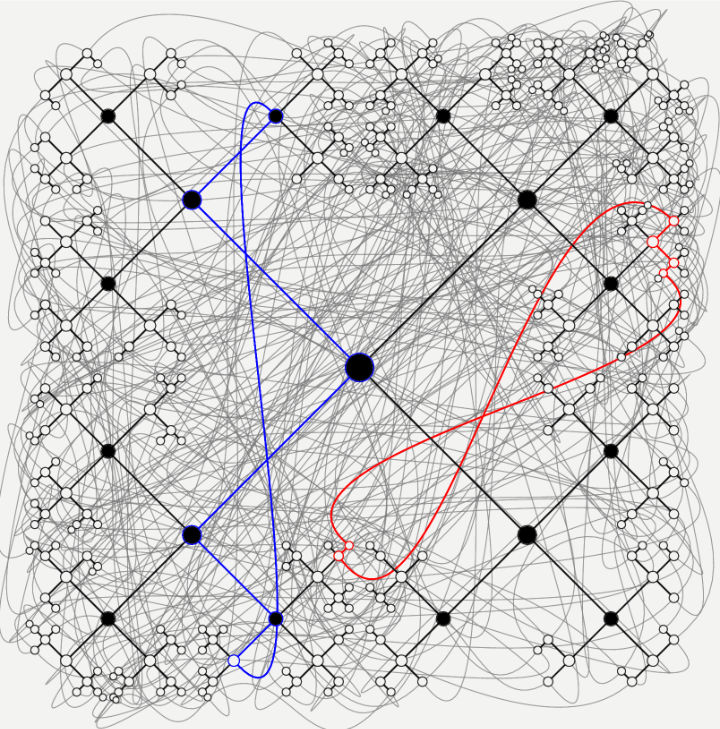
The main aim and objective of the Action is to bring together leading groups in Europe working on analytical and numerical approaches to a range of issues connected with modelling and analysing mathematical models for dynamical systems on networks (DSN), in order to be able to address its research challenges at a European level.
find out more